このシリーズ(?)では一般相対性理論が説明した1)重力による時間の遅れ 2)重力による光路の曲がり(レンズ効果)3)水星の歳差運動(近日点の移動) 4)シュワルツシルト半径の計算を特殊相対性理論を使い「ほとんど」「なんとなく」「たぶん」説明できることを示します。これらは私が18歳から19歳のときに考えたことで、今思うとかなり幼稚な内容です。その点は覚悟してください。子供の考えた大人げない相対性理論ということで、不完全な内容ですがお楽しみください。
このシリーズを理解するには最低でも特殊相対性理論の「結論」がどういうものかということを知っている必要があります。例えば物体は光速を超えることができない、とか、時間が速さによって遅れるというような内容です。数式が出てきますが、ほとんどが中学2年程度までのものなので、難しくはないと思います。それから高校1、2年程度の物理も何となく理解しているとわかりやすいと思います。例えば重力は距離の二乗に反比例するということを知っていると読みやすいと思います。(ただし水星軌道の計算だけは大学レベルです)
小さくて重い天体にボールを落としたら
今、ある天体があったとして、その天体にボールを落とす実験をします。この実験を天体から遠く離れたところからあなたがそれを観測します。なおボールは天体から極めて遠くから落下をはじめるとします。(注意:遠くからとか、小さいとかという表現が出てきますが、適当に解釈してください)
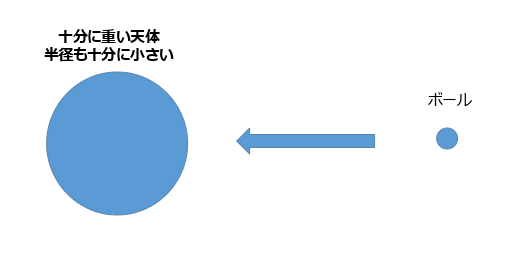
ボールはこの天体の重力により引っ張られてどんどん加速していきます。そして天体に衝突します。ボールの速さは高校の物理でも学ぶように以下の通りです。なお、数式がわからなくてもいいです。ポイントは天体に向かって落下するボールの速さは速くなるだろうということが理解できればいいです。
エネルギー保存則により
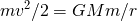
eq 1-1
変形すると
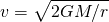
eq 1-2
ここでv はボールの速さ、Gは重力定数、Mは天体の質量、そしてrは天体の中心からボールまでの距離です。すなわち「ボールの速さは天体との距離rが小さくなると速くなる」ということです。ある意味当たり前です。さて、ここでr、すなわち天体の中心とボールの距離がどんどんと小さくなったとします。vは大きくなりますが、rが天体の半径Rになるとボールが天体に衝突するのでこの実験はここで終わります。しかしもし天体の半径が十分に小さくなったらどうでしょうか。例えばこの天体が太陽で、その半径が1kmしかなかったとします。
頭の中では天体の質量Mをそのままにして、半径Rが十分に小さいと仮定できます。するとvはいくらでも大きな値を持つことができます。数値計算はしませんが、もし太陽の半径がわずか1kmとしてボールが太陽に落下をはじめると、このボールは光速を超えてしまいます。(ガッツがある人はご自身で計算してみてください)
上のeq 1-2 のv、すなわちボールの速さを光速cとしてrについて解くと
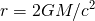
eq 1-3
ボールと天体の中心との距離はこの値になると、ボールの速さが光速になるということです。繰り返しますが、この距離は天体の質量はそのままに、半径Rを小さくすればボールが天体に衝突する前に達成でき、その時のボールは光速となります。ここまでで理解してもらいたいのは天体の半径が十分に小さいとボールは天体にぶつかる前に光速を超える、という点です。
しかし、特殊相対性理論によれば光速より速いものはありません。言い換えるとこの最後の式で計算されるrよりも小さい天体はありえない、ということです。なぜならこのrよりも小さな天体にボールを落とすとボールの速さが光速を超えるからです。ちなみにeq 1-3 は有名なシュワルツシルト半径と呼ばれているものです。アインシュタインの一般相対性理論の特殊な解の一つです。
上のリンク先にもある通り、この半径は今私たちが見た通り古典力学(アインシュタインの対性理論以前の力学)だけを使い導き出すことが可能です。しかし、古典力学と特殊相対性理論の結論を考慮すると上の「思考実験」には矛盾があります。もし光速cを超えないとしてもボールは天体と衝突するのか…cに限りなく近づくとボールの質量は特殊相対性理論の結論により、どんどんと大きくなります。ではそのエネルギーはどこから来るのか?
私はこの疑問をどうしたら解決できるかということを当時毎日考えていました。そして一般相対性理論を学ぶのが大変そうだったので、もっと簡単に理解できる方法を探ったのです。
繰り返すと古典力学的に単純なボールの天体への落下を考えると、ボールが光速を超えるということです。しかし特殊相対性理論では光速を超える物体はありません。ここには矛盾があり、これを解決するには理論に何らかの修正が必要です。
当時私は特殊相対性理論だけでこの矛盾を解決できるのではないかと子供ながらに考えていました。