天体に自由落下するボールは古典力学的にはどんどんとその速さを増していき、もし天体の半径が十分に小さければボールの速さは光速を越えるという話を書きました。しかしここで特殊相対性理論を考えると明らかにこの思考実験には矛盾があります。そこでこの矛盾を回避するために特殊相対性理論に力を借りようというところまで話を進めました。どのように力を借りるかという具体的な話を今回はします。
当時私は重力場だけでなくもっと一般的な加速場には潜在的な速さを内包しているのではないかと考えました。そこで二つの思考実験を考えてみました。今回紹介する思考実験は当時私が考えた順番とは違いますが、まずは簡単に想像できる自由落下を考えてみます。
紐のついたボールをスカイツリーの上からゆっくりと下ろしたとします。ゆっくりと下すのでボールが地面に到着したときにはボールの速さは0です。一方同じ高さからボールを自由落下させると地面に衝突する直前にはそのボールはそれなりの速さを持っています。(注意 思考実験なので空気の抵抗がないとしましょう)前者は重力を感じながらボールは移動し、後者は自由落下なので重力は感じず、地面に向かいます。
私の当時考えた仮定はゆっくりと地面に到着したボール、すなわち前者は自由落下したボールと同様に、相対論的な効果が起きるというものです。「実質同じ効果がある」ということです。少し無理がある仮定ですが、後で説明する二つ目の例を考えるとあながちこの仮定に無理があるとは思えないと当時の私は考えました。ただ、まずはこの仮定を具体例で説明するためにこの紐によるゆっくりとした移動と自由落下を考えます。
高校の物理で学んだように地表近くの自由落下はエネルギー保存則により
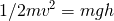
eq 3-1
ここでmはボールの質量、hは落下をはじめたときのボールの地表からの高さ、gは地表近くの重力加速度、そしてvは地表に激突するときのボールの速さです。この式からvは
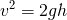
eq 3-2
となります。特殊相対性理論で登場する因子は以下のようにあらわせます。
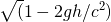
eq 3-3
この因子は自由落下したボールが地表に衝突する直前のもので、地表近くにいる観測者がこのボールの内部の時間がこの式で表されるだけ時間が遅れる、遅く流れるということです。ここまではあまり違和感がないでしょう。重力場の中での議論ですが、かなり素直な計算で拒絶反応はあまりないと思います。
ここからが当時の子供だった私の思考のジャンプです。eq 3-3 を見るとわかる通り、2ghが単位質量当たりの位置エネルギー(ポテンシャルエネルギー)の差となっています。そこで大胆にこの式を落下を始めた位置とh離れた(下でも上でもいい)位置との「相対論的な効果」と考えたのです。観測者に対して動いていなくても、自由落下ではなく加速度を感じながら位置を移動すると、この式で表せる相対論的効果が生まれる、そう考えたのです。
実際、この式の 2gh を万有引力の法則でのポテンシャルに置き換えると太陽の近くを通る光線の重力による曲がりや時間の遅れが一般相対性理論が予言した値と同じ結果が得られます。ただし上の考えを一般化する必要があります。この一般化とポテンシャルをどのように求めていくかの説明を次回以降数回で続けます。
注意 アインシュタインは1911年に等価原理からほぼ同じ式を導きだしています。1 -gh/c^2 という式で、第二項が十分に小さい場合 eq.3-3 と近似的に同じ値になります。