前回は大胆な仮説を立てました。重力などの加速場(物体の速度を変化させる力のようなもの)が存在し、そこに物体(例としてボール)を置くと加速していきます。そして速さがついてきます。私のおバカな仮説はその物体を手を添えて極めてゆっくり移動させると加速はしません。速さは変わりません。しかし「それでも」速さを得るのと同じように仮想的な速さが存在し、同じ距離を移動したときの特殊相対性理論的な効果が生じる、ということです。今回説明するのはこの仮説が結構理にかなっているかもしれない、ということです。
まずは加速場(重力場)と仮想的な速さの関係を高校レベルの物理で説明するのが今回の目的です。特殊相対性理論では相対的な速さにより慣性系(一定の速さで動く例えば電車の中)の時間の進み方や長さの変化を記述します。もし重力場の各点の「仮想的な速さ」がわかれば特殊相対性理論を重力場に拡張できることになります。ではこの仮想的な速さとは何ぞやということになります。そもそもこの「仮想的な速さ」というのは私が今回勝手に作った言葉です。いい加減でごめんなさい。
話のきっかけは回転する円盤でした。もし円盤に時計のように1~12までの数字が書いてあるとします。そしてこの円盤が超高速で回転していたとしましょう。するとその回転する円盤を観測している人から見ると、数字と数字の間が短くなります。これは特殊相対性理論の言うとことです。もしこの回転が高速近くになると円周の長さが縮まるので、同じ数字が複数別のところに現れることになります。
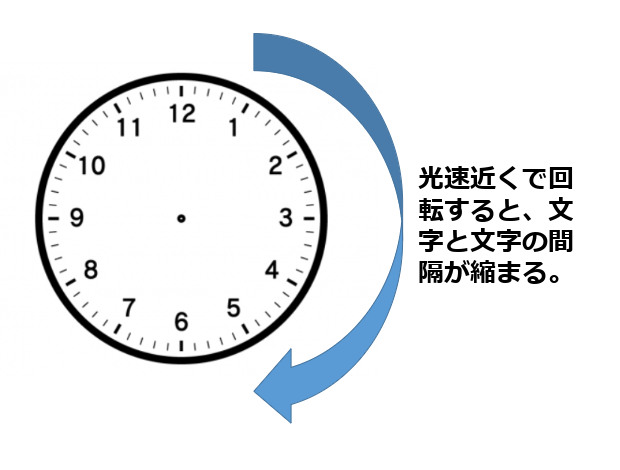
しかしそんなことはあり得ません。
この問題はエーレンフェストのパラドックスと呼ばれていて、私も彼とは独立(!)に発見していました。子供のころの話なので、許してください。そして子供なのでこのパラドックスを解決する方法を思いついたのです。円盤が回転すると(なぜか)円周方向も縮まればいいと。ばかげています。でも子供の言うのとなので許してください。
ちなみにこの話を複数の物理学者に話をしました。主だった反応です。
- そんなに高速に回転したらその円盤は遠心力により半径方向に延びるからそもそもこの思考実験は成り立たない。
- 半径方向の速さの成分がないので、特殊相対論的に半径方向に縮むことはない
- 一般相対性理論の本にもこの問題が書いてあるけど結論はないんだよなぁ
ごもっともです。しかし私はもしドーナッツ型のものが重力場で回転しているならばこの物体の半径を調節することで光速近くでも回り、かつ円周方向に遠心力で延びることもない、などと反論して大人を困らせました。どういうことかというと、例えば宇宙ステーション内は無重力です。遠心力と重力が釣り合っているからです。もし非常に長い宇宙ステーションを作り、その形がドーナッツ型であればそのドーナツ型の宇宙ステーションのどこでも無重力になるようにドーナッツの半径と速さを調整できます。その時には確実に円周方向には縮まりかつ遠心力により崩壊することもないです。どうだ、大人を言い負かしたぞ!という感じです。ちなみに今回はこのパラドックスについてはこれまでとして、先に進みます。
重力場ではなく、「普通に(慣性系に)」あるドーナッツを回転させます。すると(ここからは少し数学が出てきますが結果だけ見てもいいです)角速度ωで回転しているとすればドーナツの円周の速さは
v = ωR
eq. 4-1
となります。ここでRはドーナツの半径です。また中心から r 離れた位置の加速度 a は
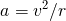
eq. 4-2
この加速度を中心からドーナッツまで積分すると
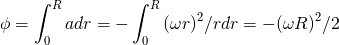
eq. 4-3
よって 4-1, 4-3 から以下が得られます。
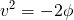
eq. 4-4
特殊相対性理論に出てくる因子Kは以下のようになります。
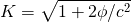
eq. 4-5
すなわち、加速度の積分φを使って、相対論的な効果を表すことができるということです。例えばφはスカイツリーの高さhと地面の間では近似値として – gh となります。これは(3)で求めた値と同じです。また、2φ/c^2 は非常に小さい値なので、近似値としては K = 1 – gh/c^2 となり、これは1911年にアインシュタインが求めた値と同じになります。
補足というか念押し 上の議論の面白いところはゆっくりとドーナッツの中心から外へ移動すると、その移動中各点で加速度を感じます。さらに「ゆっくりと移動」しているにも関わらず、重力場の場合と違い速さを獲得しています。ですから加速場、重力場の二つの点ではちょうど上の式 4-5の平方根で得られる速さを「内在している」と解釈しちゃいます。あぁ、大胆!
以前アインシュタインは特殊な例を突然一般化する、という話を聞いたことがありました。そして天才は特殊な例を見て一般化する人だということもどこかで読んだことがあります。一方凡人が何かを一般化するとろくでもない結果になります。しかし私はここで天才のふりをすることを決意をしました。この加速度(加速場)を距離で積分した値は二つの位置の間の仮想的な相対速度(速さ)の二乗の差は eq.4-4 で与えられるとしてしまいます。(ここでφは加速度を距離で積分しているので一般的にポテンシャルというような物理量となります。正確には単位質量当たりのポテンシャルです。)
この相対論的な因子が正しいのかそうでないかの判断は実際にこの一般化をいくつかの事象に応用すればわかります。しかし重力の場合、このφはどうなるのでしょうか。想像できるのは近似的に GM/r になるということです。これは古典力学、ニュートンの万有引力から簡単に導き出せます。そこでこの値を代入していくつかの計算をしてみました。
- 太陽の近くで光が曲がるとしても観測地の半分となる
- 水星の近日点の移動はやはりかなり小さくなる(たしか一世紀あたり23秒)
- しかし地表近くの時間の遅れなどは正確に計算できる(ひとつ前の記事をみてください)
これらのことから想像できるのは、重力が小さい場合は上の近似が成り立つが、重力が大きくなるとこの近似が成り立たない、ということです。実際には例えば水星の質量は上の因子分増加するので古典的な万有引力は使えないことは明白です。
ということで次回(5)では重力場におけるφを探してみます。